■学年の終わり、つまずきに注意
6年生はもう受験間近、過去問の演習などに力が入っていることと思います。
4年生、5年生も学年の終盤、12月〜1月は算数の重要単元が目白押しです。
サピックスの4年生は、規則性・速さ・平面図形・文章題など次々に重要単元が出てきます。
そして速さに関しては日能研、四谷大塚とも4年生のこの時期に学習することになります。
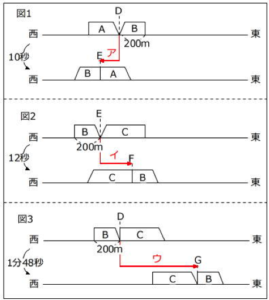
「速さ × 時間 = 距離」
という、いわゆる「は×じ=き」の公式を覚えて当てはめる子も多いのですが、公式を覚えることよりも「速さの感覚」を身につけることのほうが重要です。
「同じ速さで進み続けたら、2倍の時間進めば2倍の距離進む」
「同じ距離を進むんだったら、速さが速いほどかかる時間は短くなる」
といったことを感覚的にわかっていなければ、応用問題に対応できるようにはなりません。
大人にとっては「当たり前」のことですが、子どもにとってはそうでもないのです。
「『駅から徒歩10分』とか書いてるけど、このときの歩く速さは分速80mくらいで計算してるんだよ。徒歩10分ってことは、駅から何mくらい?」と聞いてみたり、クルマなどでお出かけする際に「今時速80kmで走っているから、この調子で行くと何時間くらいでつきそう?」など声かけするなどして、身の丈の速さの感覚を育ててあげることはとても重要です。
そして多くの塾で、この時期4年生は図形を習います。
立体図形、中でも表面積などでは計算力の弱いお子さんは「やり方は分かるけど答えが合わない」となって苦手意識が芽生えがちです。
この冬計算力を今一度見直してみるのもいいですね。
■5年生は本格的な難度の問題
サピックスの5年生は、この時期に「N進法」「ニュートン算」といった全く新しい単元の学習があります。
入試頻出ではないのですが、抽象度が高く苦手とするお子さんの多い単元です。
うまく自分の中に落とし込みたいところです。指導する先生の力量によっても、理解度が大きく変わる単元です。
一方で、各塾とも図形の学習は最重要事項の1つです。グラフを扱った問題なども出てきて「グラフが折れ曲がっている=何か変化が起こっている」という、グラフを読み取る上での基本的な感覚を身につけることが重要になります。
目まぐるしく重要単元を学習する12月〜1月ですが、6年生を控えたこの時期、どれもしっかり身につけておきたいものばかりです。
■冬のテーマを決めよう
特に5年生は、来年さらに目まぐるしくなると考えておくのがいいと思います。
社会(公民)以外の科目は、多くの塾ですでにすべての学習単元を5年生までで終えてしまいます。
だからこんなに目まぐるしいのですが、そこまで速い進度で塾がカリキュラムを組んでいるのは、6年生をまるまる1年間、受験対策に費やしたいから。
6年生は、「気がついたら夏になっていて、入試対策が始まったかと思ったら直前期になっていた」という感覚で毎日が過ぎていきます。
苦手単元がたくさん残っていても、なかなか埋め合わせをするための時間も取れない、となると思います。
冬休みも含めて12月〜1月、もう一度お子さんの手薄な単元は何かを確認し、復習の時間を意識的に取るようにしたいですね。
来年、万全のスタートを切れるよう、着々と準備していきましょう!