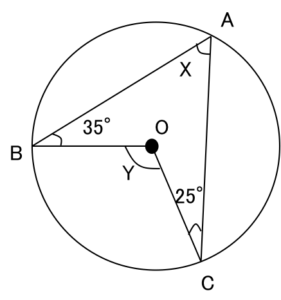
図のような角度の問題があります。XとYの角の大きさを求める問題です。
この問題を子どもたちに教えるときに「Xの角度は25°と35°の合計になります。」とまず結論を伝えて「なんでなんで?」と子どもたちの好奇心を高めて説明を展開していくか、あるいはまっさらな状態でまずはいろいろ考えてもらうか、講師によって、またクラスやお子さんによって手法は様々ですが、上手な講師ほど、お子さんを主人公にして解いていきます。
お子さんが主人公、というのはどんな様子か、ちょっとシミュレーションしてみましょう。
講師「さて、XとYの角の大きさを知りたいんだけど、どうすれば求めやすくなりそうかな?
お子さん「・・・補助線?」
講師「補助線!いいね。引くとしたらどこに引こうか。」
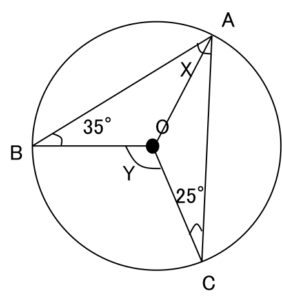
お子さん「えっと、Aのところから中心かな。」
講師「どうしてそう思ったの?」
お子さん「円の問題の補助線は中心まで、って習ったんだ。」
講師「そうなんだ。じゃ引いてみよう。」
講師「さて、なんか気づくことはあるかな?」
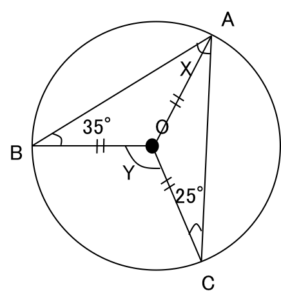
お子さん「二等辺三角形だ!」
講師「そう。円の半径はどこも長さが等しいからね。」
お子さん「そうか、二等辺三角形ができやすいからなんだね。じゃあ、Xは 25 + 35 で 60°だ!」
講師「その通り!こんどはYだね。」
お子さん「これって『ブーメラン』だよね。Yはこの3つの角の大きさの合計になるんだよね?」
講師「よく知ってるね!どうしてそうなるんだっけ?」
お子さん「ええっと、たしか外角が関係あるんだよね・・・こうやって・・・」
お子さん「こうでしょ?こっちの三角形の2つの35°の合計がここで、こっちの三角形の2つの25°の合計がここ。だから3つの合計がYですっ!」
講師「素晴らしい!(パチパチパチ)」
お子さん「エッヘン!」
ま、今どきお子さんが「エッヘン」と言うかは別として、講師がナビゲート役としてお子さんが解き進めるのをサポートしています。
『ブーメラン』についてお子さんが覚えていましたが、さりげなく理由があやふやになっていないか確認しています。
そして、もしも『三角形の外角定理』まで不安だと思ったら、さらにこの講師は確認を入れるでしょう。
あくまでも考え、解いていく主体はお子さんの方です。
だからお子さんは「解いた」という実感があり、納得感もあるでしょう。
こういう講師に習っているお子さんは、自分で勉強するときも「対話」しながらするようになります。
「えっと、ここがこうでしょ。だったらこれは3になるよね・・・そうそう、だから・・・」みたいな感じです。
自分の中に「もう一人の自分」がいて、その「もう一人の自分」と対話しながら解くんですね。
この「もう一人の自分」は、頼りになる相棒としてお子さんを助けてくれます。
「え〜、だめだよこのやり方じゃ。さっきからずっと同じところをグルグル回ってんじゃん。ちょっと視点を変えてみようよ。」
「ちょっと時間使いすぎてない?テストなんだからさ、他にできる問題を見つけてそっちをやったほうがよくない?」
ときにはこんな助言もくれます。
講師になりたての頃は、皆「教えること」に一生懸命になります。
でも、やがて「教える」というプッシュ型のアプローチから「引き出す」というアプローチに変わっていくのです。
教えて、わからせても、お子さんが解けるようにならなければ意味が無いからです。
だから「わかりやすい先生」の先に、まだ講師には目指すところがあるのだと思っています。
そんなことを考えながら、主催する「名門指導会」の先生方との勉強会を常に続けていこうという思いを強くする春です。
お子さんたち「もう一人の自分」はいるでしょうか。
ちょっと確認してみてあげてください。










コメントを残す